More Hacks at Hack the North CTF Two

18 Sep 2015

We the lurkers of the Hack the North #random Slack channel were once again in the midst of another CTF on September 12th, a mere four days after the first one fell. With 10 winning spots on the line, people from far and wide came out for the final challenge.

First time here? Don’t forget to check out my log post on the first Hack the North CTF!

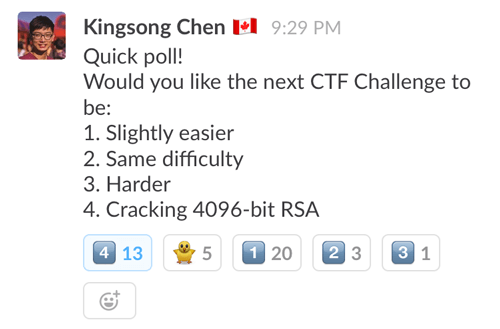
A few days earlier, one of Hack the North’s organizers put out a poll on how hard the next CTF should be. A majority voted for a CTF easier than the first one, though an option to break 4096-bit RSA did come close to winning.

The CTF’s admins promised that their new CTF would be more straightforward than the last one, and encouraged us to work together instead of asking them privately for hints. This lead to a more collaborative CTF, and the #random channel was alive with discussion about the clues people found. This post outlines my experiences during the CTF.

I was actually late to the party, only starting the CTF on Sunday at 1am EDT since it was the weekend before classes at Waterloo. I had a lot of help and hints available by then. :P

The Aftermath of CTF One

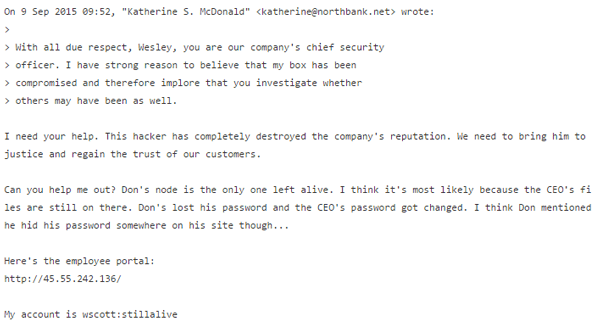
The CTF begins with a pastebin message from wscott, the North Bank’s Chief Security Officer (CSO). In it, we see a picture of the North Bank after the devastating results of the first Hack the North CTF. The company’s reputation has gone down the drain and they have gone on lockdown to secure as much as they can. The CSO has unwittingly contacted us to help track down the hacker responsible for this and bring him to justice. He helpfully provides us with his username and password to the bank’s Employee Portal.

From the first CTF, we know that we were hired by a mysterious hacker named J, who (in the story) tricks us into hacking the North Bank for him. We can therefore investigate the scene of the crime to look for clues he may have left.

These Aren’t the Files You’re Looking For

After logging into the Employee Portal, we are greeted with a message that the site’s functionality has been locked down. This can be confirmed by modifying the page’s accesslevel cookie: nothing happens even when we change the integer in it. As usual, there is a link to the webmaster’s personal site.

Clicking on the essay link brings us to a long nonsensical essay on “The Weatherization of Journalists”. Scanning through this page, there appears to be nothing of use, and the length and randomness of the text implies that what we’re looking for isn’t here. Going back to the webmaster’s filesystem at /~dglenn/private/ also gives us nothing of use.

Going back to the essay page, we can analyze the source code to see if there’s anything interesting there. Another quick scan through reveals something interesting: the webmaster’s password is embedded in the page as a comment.

We can use this password to login to the webmaster’s account, which has a list of username and password combos in plaintext, including the CEO’s. We can then login to the CEO’s account, where we can download a ZIP file. Inside this ZIP file is the following image of HAL 9000 from 2001, A Space Odyssey.

At some point, the people at #random decided to open the image in a text editor. Inside was some sort of hash that started with FBMD – it was assumed that it was to be used in another part of the CTF, but it turned out that it was just a tag automatically added to Facebook photos. Undeterred, the ZIP file itself was opened in a text editor, which yielded much more interesting results:

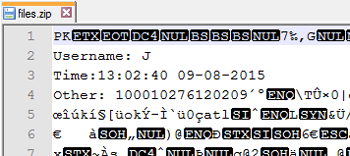
We have three fields given to us: Username, Time, and Other. The CTF admins revealed that the value for Time is just a reference for when the first CTF was beaten for the first time, so the only fields we’re concerned about are Username and Other. The tag added to the HAL 9000 file turned out to be a clue for what to do with the Other value – it’s actually the ID for our mystery hacker’s Facebook profile!

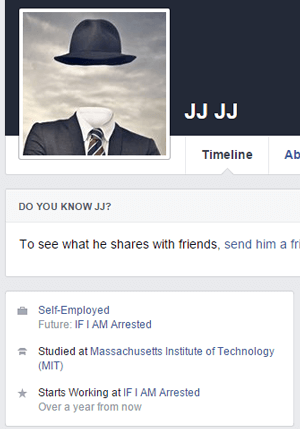
Poking around J’s Facebook profile, we can find additional puzzles to help us uncover his identity. The next two sections will look into these puzzles.

Bogocompress

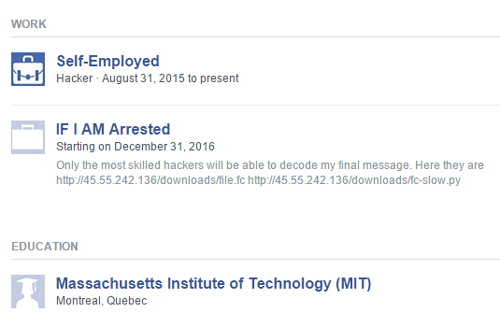
If we go to J’s Work and Education info, we can find that there’s an entry called “IF I AM Arrested”. Under this is a message giving us links to two files – file.fc and fc-slow.py.

When we open file.fc, we get a gigantic block of gibberish:

In fc-slow.py we get an explanation of what the files are used for: the Python3 file contains the North Bank CSO’s fast compress algorithm. The script uses the NumPy library, so someone in #random recommended that we install Anaconda (which contains NumPy) in order to run the script. Even then, we cannot run the script due to runtime errors, so it looks like we’ll need to further investigate what it does.

The Python interpreter complains about the following line in fc_slow.py, which can be found inside a function called s_decompress with an input parameter x:

head, body, foot = x.split('\n')

The interpreter says that there are too many values to unpack. Upon investigation, we find out that the contents of file.fc are read and converted into a list by splitting the file at every newline. This list is then passed to s_decompress, where it fails at the above line. When we look at file.fc, we find that there is an extra newline at the very end of the file. This means that when the file is split, it results in a list containing four elements, instead of the three that x.split('\n') expects. There are two solutions to fix this: we can either simply remove the extra newline from file.fc, or we can add another variable after foot in the above line.

That’s not all however. Even though we can finally execute the script, it seems that it immediately gets stuck in an infinite loop. We will therefore have to go through the script and fix anything that is implemented weirdly. This turned out to be the most frustrating part of the CTF. Everyone at #random ended up working together to overcome it.

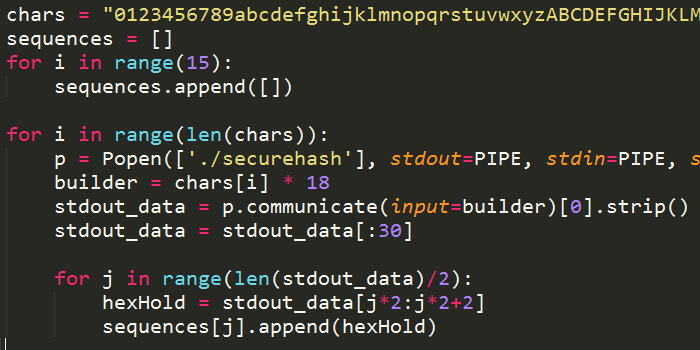
For reference, the script works as follows. The following functions exist: matmul (matrix multiplication), matdiv (matrix division), s_compress (the fast compress implementation), s_decompress (the fast decompress implementation), r_sort (a non-destructive sort function), s_encrypt (encrypts passed in plaintext), s_decrypt (decryptes passed in encrypted text) and s_securehash (the securehash implementation discussed in the first CTF post). We can add print statements to each function to figure out where the script is getting stuck.

The compression process works as follows. The program reads a plaintext file and encrypts it using s_encrypt. It then takes this encrypted string and compresses it using s_compress, which uses some random process to compress the data. It then creates a new file called file.fc that contains the compressed data as well as the information needed to decompress it. The decompression process works in reverse: s_decompress decompresses the target file then s_decrypt decrypts the resulting encrypted text. Both s_compress and s_decompress use matmul, matdiv, r_sort and s_securehash in some way in their process.

Someone first pointed out the r_sort function, which has the following implementation:

def r_sort(lst):
    """Return a clone of the list in sorted order."""
    clone = lst[:]

    while True:
        try:
            random.shuffle(clone)
            for i in range(len(clone)):
                for j in range(len(clone)):
                    if j > i and clone[j] < clone[i]:
                        raise NotSortedException()
        except:
            pass
        else:
            return clone

It is immediately obvious that this is a variation of our favourite sorting algorithm – bogosort! What bogosort does is it randomly shuffles the contents of a list until it gets a permutation where the list is sorted. Normally, bogosort has a best-case efficiency of O(n), but one of the CTF admins pointed out that this implementation is O(n²) due to the two nested for loops it uses to check if the list is sorted.

Based on the comments for this function, we can replace the implementation with the following:

def r_sort(lst):
    """Return a clone of the list in sorted order."""
    clone = lst[:]
    return sorted(clone)

This returns a sorted version of the parameter lst without destroying the original lst variable.

The second function mentioned in the channel was matdiv, which is used for matrix division operations in compressing or decompressing a file. The original implementation is as follows.

def matdiv(c, b):
    dim = len(b), len(b[0])
    maxv = 0
    while True:
        maxv += 1
        for i in range(maxv ** 2 * dim[0] * dim[1] + 10):
            cand = [
                [random.randint(0, maxv) for _ in range(dim[0])]
                for _ in range(dim[1])
                ]
            if matmul(cand, b) == c:
                return cand

As you can see, simply generating random numbers and checking to see if the matrix you found is a valid answer isn’t a good way to math. Fortunately, the script uses the NumPy library, so we can use that to our advantage. Our initial implementation was the following:

def matdiv(c, b):
    return numpy.divide(c, b)

Despite this, we were still seeing weird errors in the functions calling matdiv. Thinking that these functions were also defective, we spent a considerable amount of time stepping through them and investigating the file input to see what was defective. It turns out that our fix for matdiv is invalid – a CTF admin pointed out that numpy.divide() actually does an element-wise division (meaning that it simply divides each element in the matrix with another integer) instead of doing actual matrix division. Someone in the channel suggested to take advantage of the following matrix property instead:

We can therefore change our matdiv implementation to the following:

def matdiv(c, b):
    return numpy.rint(numpy.dot(c, numpy.linalg.inv(b)))

We call on numpy.rint() since numpy.dot() returns a matrix with floats. In our case, we’re using the results of matdiv as indices to a list, so we want the results as integers instead.

With this implementation, we find that matdiv is finally working properly, and we can move on to the next function.

Since there appears to be a common theme of bogo-esque functions screwing up the script, we can focus our search for functions that exhibit this behaviour. We don’t have to look for long – we find that s_decrypt employs a bogo-esque technique:

def s_decrypt(encrypted, key):
    """Decrypt a STRONGENCRYPTed string."""
    plaintext = []

    while encrypted != s_encrypt("".join(plaintext), key):
        plaintext = []

        for i, c in enumerate(encrypted):
            if i % 2 == 0:
                continue  # even numbers are just ABC, irrelevant to encryption
            k = key[i // 2 % len(key)]
            possibilities = []
            try:
                possibilities.append(chr(ord(k) - ord(c)))
            except:
                pass
            try:
                possibilities.append(chr(ord(k) + ord(c)))
            except:
                pass
            try:
                possibilities.append(c)
            except:
                pass
            plaintext.append(random.choice(possibilities))

    return "".join(plaintext)

This is an intimidating function at first glance. It tries to break the encrypted string by going through each character and generating a list of possibilities from it. It then randomizes this until it gets the correct original plaintext.

My initial implementation to fix this was to remove the randomization process and force the function to go through all possibilities and look for the original plaintext. This would result in an extremely inefficient function that will take a while to go through all permutations. The people who finished this part of the CTF hinted that the script was supposed to run instantaneously, and recommended that I try to reverse the initial encryption process. Once we take a look at s_encrypt, we see:

def s_encrypt(plaintext, key):
    """Use the STRONGENCRYPT algorithm to encrypt the plaintext."""
    encrypted_plaintext = []
    for i, c in enumerate(plaintext):
        e = key[i % len(key)]
        if ord(c) < ord(e) - 32:
            encrypted_plaintext.append('A')  # type A encryption
            encrypted_plaintext.append(chr(ord(e) - ord(c)))
        elif ord(e) < ord(c) - 32:
            encrypted_plaintext.append('B')  # type B encryption
            encrypted_plaintext.append(chr(ord(c) - ord(e)))
        else:
            encrypted_plaintext.append('C')  # type C encryption
            encrypted_plaintext.append(c)

    return "".join(encrypted_plaintext)

Facepalm. This isn’t hard to break – what it does is that it goes through each character of the plaintext and decides to use one of three possible “encryption” methods. For each character position, there is a possible key character that can be used to “encrypt” the character by subtracting the key character from the plaintext character in some manner (this is done by converting the characters to their ASCII number first, subtracting, then converting back into a character). Since the key is provided to us, we can easily reverse this “encryption” with some simple math:

def s_decrypt(encrypted, key):
    print("I'm in decrypt!")
    """Decrypt a STRONGENCRYPTed string."""
    plaintext = []

    for i in range(len(encrypted) // 2):
        e = key[i % len(key)]
        if encrypted[i*2] == 'A':
            plaintext.append(chr(ord(e) - ord(encrypted[i*2+1])))
        elif encrypted[i*2] == 'B':
            plaintext.append(chr(ord(e) + ord(encrypted[i*2+1])))
        elif encrypted[i*2] == 'C':
            plaintext.append(encrypted[i*2+1])

    return "".join(plaintext)

With no other bogo-esque functions in the script, we can now try decrypting file.fc. The script finishes instantly, which is a good sign. Opening the decrypted file, we get this message from J:

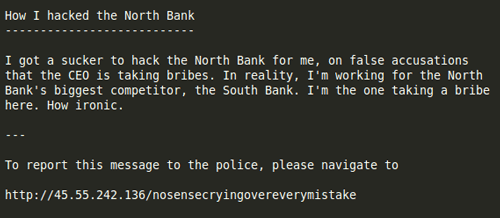
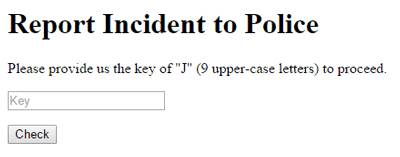
Wow. Fortunately, J is nice enough to give us a link to report him to the police. Opening this link, we get a simple page asking for J’s key, which consists of 9 capital letters. We don’t have much else to work with right now, so we’ll go back to this at a later section.

Hidden in Plain Sight

Once we go back to J’s Facebook profile, we can find a challenge posted on his wall:

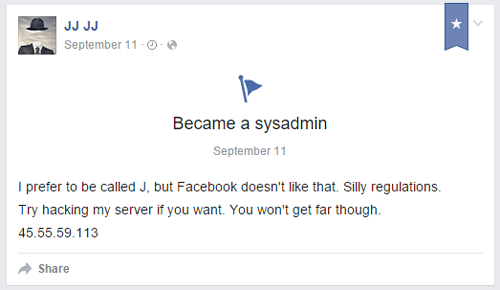
It’s an IP to J’s server! Someone in the channel ran a scan against it and found that the server only had its SSH ports open. We can guess that J’s username is (of course) J, but what about the password? One potential clue is that J has apparently been on the move all over the world:

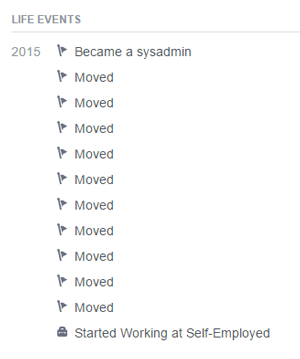
Each “Moved” life event on Facebook has a coordinate attached to it. The locations are scattered all over the world, from the streets of Seattle, WA to the rural fields of Austria. There are 10 move events in total, so it probably doesn’t correspond to the police-reporting password from before. One of the coordinates is actually repeated twice, which could be something interesting.

Everyone at the #random channel pored over the coordinates for hours: plotting them on maps, grabbing their street addresses or even adding the coordinates together. None of them turned up anything useful. Eventually, I made a sarcastic joke on the channel:

To my surprise, someone replied a few minutes later that they got into the server and found some files. Wut? I decided to double check one of the coordinates on Google Maps to see what was up.

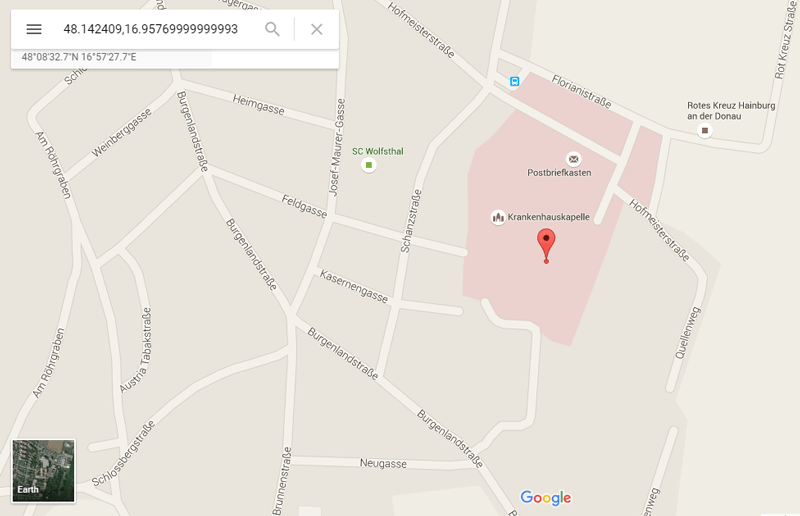
Out of curiosity, I switched over to Earth view and found this:

The coordinate is actually smack dab in the middle of a building shaped like a P! If we go through the coordinates on J’s Facebook profile in order, we can find that each is centered on a building shaped like some letter or number. Once we do that, we get a string that turns out to be the password to J’s server!

I immediately informed the #random channel about this and moved on to the next step of the CTF.

Should’ve Paid Attention in Lin Alg

Once we login to J’s server, we can find four files: instructions.txt, ciphertext, psk and grid1to26. The instructions file gives us the following information:

• The secret key is contained somewhere in the files.
• The grid in grid1to26 must be decrypted to get this key, but the key to decrypt the grid isn’t anywhere.
• “Z = (1,1) and Q = (26,1)”
• The grid’s absolute origin is at (x,y) = (8,15)
• The key’s basis is [(3,1),(-2,1)]
• Nine (!) vectors given in the standard basis: (2,1),(2,3),(4,6),(0,-2),(0,-1),(5,7),(4,8),(5,2),(2,-3)

ciphertext contained the string ZEBRVJWBMQHOIVWNUTKNOGGWPQ (not unique letters, but it has a length of 26), psk contained a list of 26 integers counting from 1 to 26 and grid1to26 contained a 26-by-26 grid of uppercase letters (available on GitHub).

I recognized that this stage would involve changing the basis, which I actually learned last term in MATH 215. Unfortunately, I had completely forgotten about the process to do that after going through four months of co-op. Oops.

At this point, I wasn’t sure how to go forward so I decided to step back for a bit and take care of some errands (this was during the weekend before classes at Waterloo after all). While waiting for a bus somewhere in Waterloo, I checked Slack to see how everyone was doing and saw that the CTF had already been beaten. Damn! @coruon, who was part of the team who first beat the first CTF, was once again the first to beat this CTF. He was followed by Ryan H., who was the third person to finish the first CTF (after us).

Fortunately, there were still seven other spots to get! The two winners gave some hints: to decrypt the grid, we would have to reorder some parts of it, the end goal of decrypting was to make the the first row of the grid equal ciphertext, and that the change of basis instructions was not related to decrypting the grid.

Looking at ciphertext, we can see that it has 26 letters, which matches the size of the grid. At first glance at the grid, it seems that setting ciphertext as the first row is impossible: for example, the first letter in ciphertext, Z, simply did not exist anywhere near its supposed position. I even tried doing some mapping – since psk was made up of a list of 26 unique integers from 1 to 26, I thought that a Caesar cypher mapping (i.e. each letter is replaced by a corresponding one) was being used to encrypt the grid (unfortunately, this did not produce anything).

Looking closely at the letters in the grid revealed something interesting: the first column where a Z appears is the third column. This seems to correspond to the first integer in psk: 3. This pattern continued to repeat for each letter in ciphertext and each number in psk. That’s when I realized it: the columns in grid1to26 will have to be ordered as specified in psk. To actually create ciphertext in the first row, we will have to shift the letter in each column, much like one would with a dial.

I quickly wrote a script to test this idea. The script is available on GitHub – in its current form, the script can actually solve the entire puzzle, but at the time it only produced the reordered and shifted grid, and I continued the rest of my idea by testing manually.

Assuming that the top-left is (1, 1) (as specified in the instructions), we can set the absolute origin to be at (8, 15). From there, we can treat the grid as a normal Cartesian plane, where the origin is (0, 0) and where the x- and y- axes intersect. This is shown in the following diagram.

From here, we can start with the change of basis process. It’s been a while since I actually did this, so I had forgotten how to actually change a coordinate from one basis to another. Fortunately, @coruon posted this helpful guide in changing the basis. Even then, I still messed up the process – fortunately, a CTF admin was there to guide me through the math (thank you!).

Since we’re changing the basis from the standard basis to our target basis, we can simply use the following equation:

Using Microsoft Math (I apparently no longer had access to Matlab on the university computers), I went through each vector given in the instructions and multiplied them with the transformation matrix to get the actual vector. Given each vector, I went through the decrypted grid and came up with their corresponding letters.

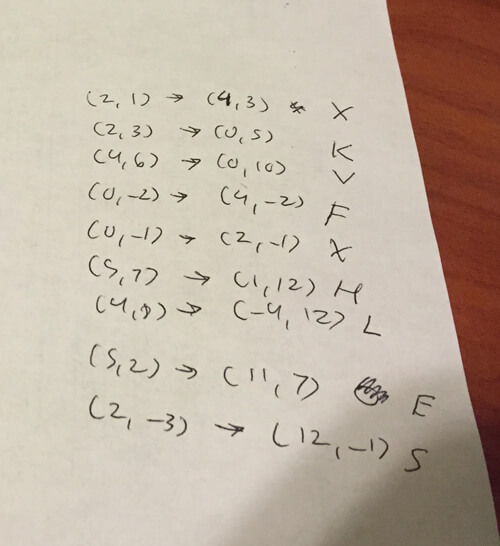
Once we convert each basis-changed vector into their corresponding letters, we get a string of nine uppercase letters. We can copy-paste this into the police reporting page from before, after which we finally defeat CTF Two. Victory!

Final Victory

I ended up being the third person to beat the CTF, about an hour and a half after Ryan H.

Over the next few days, the other winners and I ended up helping out anyone else still working on the CTF by giving out hints and even helping them out on technical issues. All 10 spots were finally taken on September 17th, five days after CTF Two’s launch and just a day before the start of Hack the North.

I honestly had a lot of fun with this CTF! It was great working with everyone in solving each puzzle, and it was a great refresher for the start of the school term.

The top winners were promised black forest cake at Hack the North, but it turned out that the cake is a lie. We did get a plush of Waterloo’s favourite mascot: the Canada goose.

Once again, thank you so much to the CTF admins for making such a fun puzzle on short notice, and for being there 24/7 to help us out with issues. You guys are awesome!

I’d also like to thank everyone who played along with the CTF, and worked with everyone to solve each puzzle. Good luck at Hack the North!